THE BEAUTIFUL RATIONALITY OF Π,
√2,
& Φ
PI Rational PI
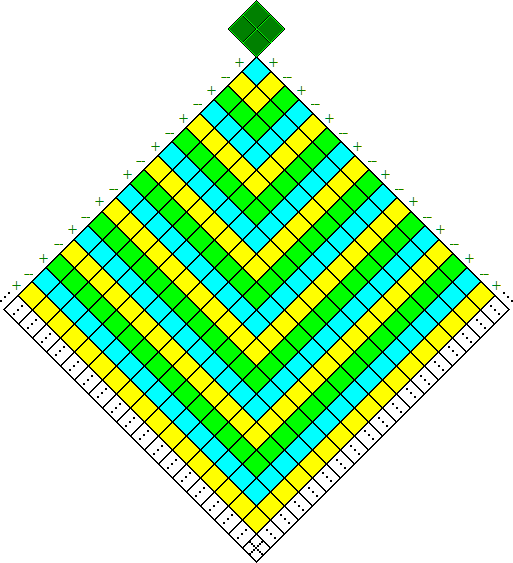
Where π = + (4/1) + (4/-3) + (4/5) + (4/-7) + (4/9) + (4/−11) + (4/13) + (4/−15) + (4/17) . . ., π is the sum of an infinite repetition of the four-square successively divided by the number of squares on the leading edge of an infinitely expanding square of squares beginning with one-square, which number of squares––though always odd itself––is negative when not the leading edge of the square of an odd number of squares.
Every partial sum of this series is itself a rational number: (4/1) = 4, (4/1) + (4/-3) = 8/3, (4/1) + (4/-3) + (4/5) = 52/15, (4/1) + (4/-3) + (4/5) + (4/-7) = 304/105, (4/1) + (4/-3) + (4/5) + (4/-7) + (4/9) = 1052/315, (4/1) + (4/-3) + (4/5) + (4/-7) + (4/9) + (4/−11) = 10312/3465, (4/1) + (4/-3) + (4/5) + (4/-7) + (4/9) + (4/−11) + (4/13) = 147916/45045, (4/1) + (4/-3) + (4/5) + (4/-7) + (4/9) + (4/−11) + (4/13) + (4/−15) = 407712/135135, (4/1) + (4/-3) + (4/5) + (4/-7) + (4/9) + (4/−11) + (4/13) + (4/−15) + (4/17) = 7471644/2297295, . . ..
And the denominator of a rational partial sum is the product of the absolute values of the last x denominator(s) in the π series to that point, where x successively equals 1, 2, 3, 3, 3, 4, 5, 5, 6, 7, 8, 9, . . .. The product of the absolute values of the numerator(s) and denominator(s) of the last x ratios in the π series at the point of a rational partial sum divided by the denominator of that rational partial sum = 4x, where x successively equals 1, 2, 3, 3, 3, 4, 5, 5, 6, 7, 8, 9 . . ..
Compare the 4-numerator of this simplest of the infinite series equal to π with the notion that "the constant identity of the system of reference, the identity of the system of reference as the center, is the numerator" (D.G. Leahy, Foundation: Matter the Body Itself [Albany, 1996], pp. 485ff.), and with the 4-fold structure of the hyperlinear vertex that is the unique hypercubic rational constitution of the absolute dead center cube (The Deep Epidermal Surface: The Cornerstone Construction Order, Minimum Order Tetrahedron Hypercube, & Absolute Dead Center Hypercube), whose definition is (x/6)4/x3 = 8x3/x4 (= [√2×9]−1 = √162−1) (where φ is the division in extreme and mean ratio, this definition of the absolute dead center cube = [(φ×10162)1/162]1/[162(√162/2)2]/10 × π/4 accurate to 1 part in 100 million):1
Reality is essentially
rational. π is the area of the circle circumscribing the square whose area is 2
on the diagonal of the square whose area is 1. The ratio 2 : 1 is
the foundation of all irrationality. Hence the rational derivation of
√2 here
illustrated:
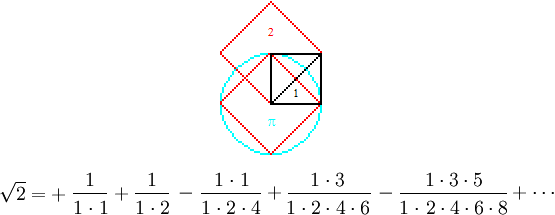
Like π,
√2 is perpetually
rational, as illustrated in the above series, each element of which is
positive (+) where the number of numbers in the denominator is even and
negative (–)
when that number is odd. Indeed, as here illustrated
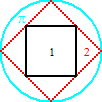
qua
inscribing : inscribed areas, π : 2
:: 2 : 1, the proof of which proportion is precisely
Like π and √2, φ, the division in extreme and mean ratio, where AB : AC :: AC : CB, is also a function of the 2 : 1 (here, the 1-square transformed to a triangle, linear) ratio and perpetually rational as here illustrated:
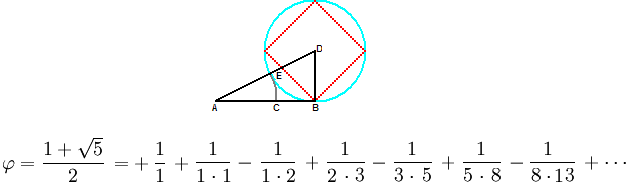
Each element of this series is positive (+) unless it has an immediate predecessor whose denominator is the lesser and the difference between the two is 1 less than the sum of all the preceding denominators including that of its immediate predecessor, in which case it is negative (–).
Note
1
It is uniquely true for the absolute dead center cube that [(x/6)4/x3]2
= (8x3/x4)2 = 162−1
(cf., on this web,
Theorem & Proof: The Uniqueness of the Absolute Dead Center Cube). 162−1 = the
rational product of הארץ המבטחת,
“The Promised Land.” The perfectly hypercubic rational constitution of
the absolute dead center cube is demonstrated by the fact that it is
uniquely true for it that [(x/6)4/x3]-4
= (8x3/x4)-4
= 1622 (ibid.). The integral product of
שכל גמור, “Absolute Intellect,” =
1.622 × 1010, its rational product is (
× 10−1)−1
(cf. the rational product of Genesis 1:1,
בראשית ברא אלהים את השמים ואת
הארץ, “In the beginning God created
the heaven and the earth," × 10-7
[cf. D.G. Leahy,
Foundation: Matter the Body Itself
(Albany,
1996), p. 505]), and its linear product is 2.592 ×
1010 (cf. the area of one quadrant of the face of the
absolute dead center cube, 2592 [ibid., pp. 433ff.]). For
השכל
הגמור as
Maharal’s term for Torah, cf. E.R. Wolfson, Aleph, Mem, Tau:
Kabbalisitc Musings on Time, Truth, and Death (Berkeley,
2006).
