Revelation 21:16−17: “The city was laid out as a square, its length equal to its breadth. The angel measured the city with a rod and it was 12000 stadia in length and breadth and height. He measured its wall, and this was 144 cubits high, according to the human measure he used.”
The locus of the φ-spiral inscribed in the ‘golden rectangle’ the sides of which equal, respectively, 1 and φ, is at 1.170820378 (= φ2/51/2) times the length of the side of the square at each stage of the infinitely φ-diminishing square in the direction of the turn of the spiral (see, on this web, The Golden Bowls & the Logarithmic Spiral):
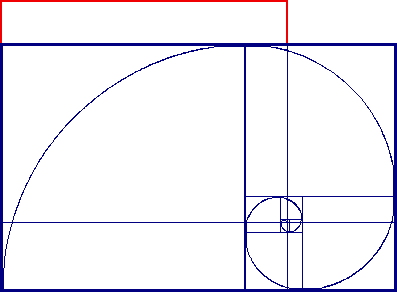
Where a cubit = .457 m,1 a stadion = 185 m,2 the height of the wall of the New Jerusalem square = 144 cubits = 65.808 m, and the length of one side = 12000 stadia = 2220000 m, the total metric area of the New Jerusalem 4 walls ~
1.170820378128 m2.
Where the New Jerusalem square is set in the center of the square whose edge passes through the locus of the logarithmic spiral as measured from the side of the New Jerusalem square (see above),

and where x is the edge of the absolute dead center cube for whom it is uniquely true among all cubes that [(x/6)4/x3]-8 = (8x3/x4)-8 (see, on this web, Theorem & Proof: The Uniqueness of the Absolute Dead Center Cube), the total metric area of the 4 walls surrounding the New Jerusalem square = 65.808 m × (2220000 m × 1.170820378) × 4 =
684198205.2 m2 ~ 685410196.6 m2 = (100φ)4 m2
~ [(x/6)4/x3]-8 m2 = (8x3/x4)-8 m2.
Notes
1
The New Jerusalem Bible, ed. H. Wansbrough (New York and London, 1985),
p. 2077.
2 Ibid.