BANACH-TARSKI PARADOX & THE REAL TRINARY LOGIC
MATRIX OF THE FIBONACCI, GEOMETRIC,
& PERFECT NUMBER SERIES
“A ball can be decomposed into a finite number of point sets and reassembled into two balls identical to the original.”
“The Banach–Tarski paradox is a theorem in set theoretic geometry which states that a solid ball in 3-dimensional space can be split into a finite number of non-overlapping pieces, which can then be put back together in a different way to yield two identical copies of the original ball. The reassembly process involves only moving the pieces around and rotating them, without changing their shape. However, the pieces themselves are complicated: they are not usual solids but infinite scatterings of points. A stronger form of the theorem implies that given any two 'reasonable' objects (such as a small ball and a huge ball), either one can be reassembled into the other. This is often stated colloquially as 'a pea can be chopped up and reassembled into the Sun'. . . .
“The reason the Banach–Tarski theorem is called a paradox is because it contradicts basic geometric intuition. 'Doubling the ball' by dividing it into parts and moving them around by rotations and translations, without any stretching, bending, or adding new points, seems to be impossible, since all these operations preserve the volume, but the volume is doubled in the end.
“Unlike most theorems in geometry, this result depends in a critical way on the axiom of choice in set theory. This axiom allows for the construction of nonmeasurable sets, collections of points that do not have a volume in the ordinary sense and require an uncountably infinite number of arbitrary choices to specify. . . .2
“It was shown in 2005 that the pieces in the decomposition can be chosen in such a way that they can be moved continuously into place without running into one another. . . .
“Using the Banach–Tarski paradox, it is possible to obtain k copies of a ball in the Euclidean n-space from one, for any integers n ≥ 3 and k ≥ 1, i.e. a ball can be cut into k pieces so that each of them is equidecomposable to a ball of the same size as the original.”
1 = Infinitely Dense Sphere, K = Keeper, M = Decompose & Reassemble, MM = M Iterated Once
1,
0, 
, 1 = Real
Trinary Logic Respective Digit Analogues3
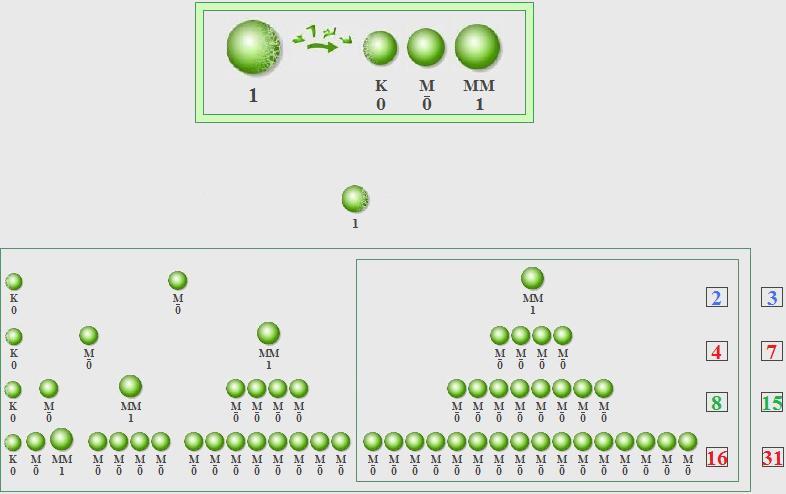
et cetera, ad infinitum.
Compare the Iterative Sequential Summing of the Real Trinary Logic Geometric Series, Matrix of the Numerical Geometric and Perfect Number Series
(For a full exposition available on this web click on the image)
et cetera, ad infinitum.
Compare the Real Trinary Logic Sequence Appearing as the Central “Trunk” of the Fibonacci Rabbit Tree
(For a full exposition available on this web click on the image)
et cetera, ad infinitum.
Notes
1 Complete
text available at:
http://en.wikipedia.org/wiki/Banach%E2%80%93Tarski_paradox.
2 The axiom of choice (http://plato.stanford.edu/entries/axiom-choice)
stipulates that the collection of sets from each of which a member can be chosen
is a collection of nonempty sets. This explains how it is that the
Banach-Tarski paradox is able to be shown to be consistent with real trinary
logic for which 0 ≠ nothing.
3 For the original exposition of
the logic, where 1 = (0
1) =
(0 =
= 1), cf. D.G. Leahy, Foundation: Matter the Body Itself
(Albany, 1996), pp. 255ff. Cf. also, D.G. Leahy, Beyond Sovereignty: A
New Global Ethics and Morality (Aurora, 2010) forthcoming.