__________________________________________________________________________
REAL TRINARY LOGIC GEOMETRIC SERIES
MATRIX OF THE NUMERIC GEOMETRIC SERIES &
THE SERIES OF PERFECT NUMBERS
xlogic
ϵ (0,
![]() , 1) → xmath ϵ (2, 4)
→ (xmath
= 42) → (xmath
= 3)
, 1) → xmath ϵ (2, 4)
→ (xmath
= 42) → (xmath
= 3)
__________________________________________________________________________
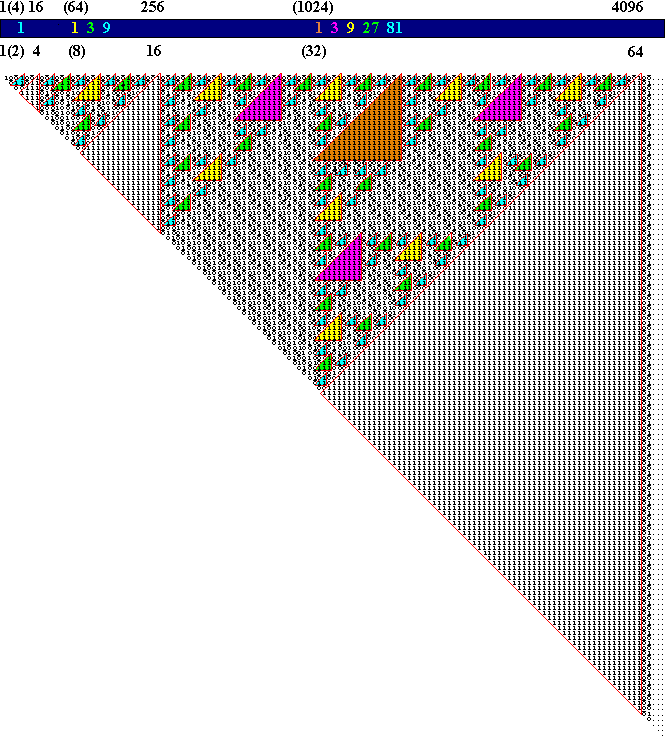
The .125 root or power is to be understood to be especially fundamental because it is the base power of the denominators of the infinitely alternating sequence of the infinite series of natural numbers and the infinite series of odd numbers which produces the infinite lattice composed of the natural numbers, the differences of their squares, the differences of the squares of those differences, the differences of the squares of those differences, ad infinitum.1 The series of the exponents of the denominator .125 in this infinite lattice is a double series composed by sequential summing. The exponents of .125 in the odd-numbered rows of the lattice are 0, 1, 1 + x, 1 + x + x2, 1 + x + x2 + x3, . . ., and, in the even-numbered rows, their respective doubles, where x = 4.
Now, infinitely iteratively sum sequentially, according to the rules
governing the relations of the trinary logic digits,2 the
initial infinitely repeating series underlying the L series,3 1, 0,
![]() , 1, 0,
, 1, 0, ![]() , 1, 0,
, 1, 0,
![]() , 1, 0,
, 1, 0, ![]() , . . . , itself the trinary logic
analogue of the geometric series, x0,
, . . . , itself the trinary logic
analogue of the geometric series, x0,
![]() , x1, x0,
, x1, x0,
![]() , x1,
x0,
, x1,
x0,
![]() , x1,
. . ., where x = any of the three logical digits.4 In the illustration above the second row is the sequential sum of the first, the
third of the second, the fourth of the third, etc. (Initial 1 is not repeated
automatically since in the trinary logic there is no implicit zero equal to 'nothing'.)
Notice the triangles filled with 1's. Only three in this picture share the long diagonal
edge of the picture. If that long edge is
examined, it will be found to consist of 1,
, x1,
. . ., where x = any of the three logical digits.4 In the illustration above the second row is the sequential sum of the first, the
third of the second, the fourth of the third, etc. (Initial 1 is not repeated
automatically since in the trinary logic there is no implicit zero equal to 'nothing'.)
Notice the triangles filled with 1's. Only three in this picture share the long diagonal
edge of the picture. If that long edge is
examined, it will be found to consist of 1, ![]() , 0; 1, 1, 1, 1 (the
shared edge of the first triangle),
, 0; 1, 1, 1, 1 (the
shared edge of the first triangle), ![]() , 0,
, 0,
![]() ,
0,
,
0, ![]() , 0,
, 0, ![]() , 0; 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1 (the shared edge of the second triangle),
, 0; 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1 (the shared edge of the second triangle),
![]() , 0,
, 0, ![]() , 0,
, 0, ![]() , 0,
, 0, ![]() , 0,
, 0,
![]() , 0,
, 0, ![]() , 0,
, 0, ![]() , 0,
, 0,
![]() , 0,
, 0, ![]() , 0,
, 0, ![]() , 0,
, 0,
![]() , 0,
, 0, ![]() , 0,
, 0, ![]() , 0,
, 0,
![]() , 0,
, 0, ![]() , 0,
, 0, ![]() , 0; 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1
(the shared edge of the third triangle). There follows in this infinite expansion a set of
64 sets of
, 0; 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1
(the shared edge of the third triangle). There follows in this infinite expansion a set of
64 sets of ![]() , 0's (not shown for lack of space). This is the
beginning of a double series of 1's and
, 0's (not shown for lack of space). This is the
beginning of a double series of 1's and ![]() , 0's, the arithmetic
transcription of each of which series, according to the logical rule that
, 0's, the arithmetic
transcription of each of which series, according to the logical rule that
![]() and 0 each = .5, is 1 + 4 + 16 + 64 . . ., the ordinary sequential
summing of which produces the exponents in the odd-numbered rows of the lattice above
mentioned, while the two series added together give 2 + 8 + 32 + 128 . . ., the sequential
summing of which produces the exponents in the even-numbered rows.5
and 0 each = .5, is 1 + 4 + 16 + 64 . . ., the ordinary sequential
summing of which produces the exponents in the odd-numbered rows of the lattice above
mentioned, while the two series added together give 2 + 8 + 32 + 128 . . ., the sequential
summing of which produces the exponents in the even-numbered rows.5
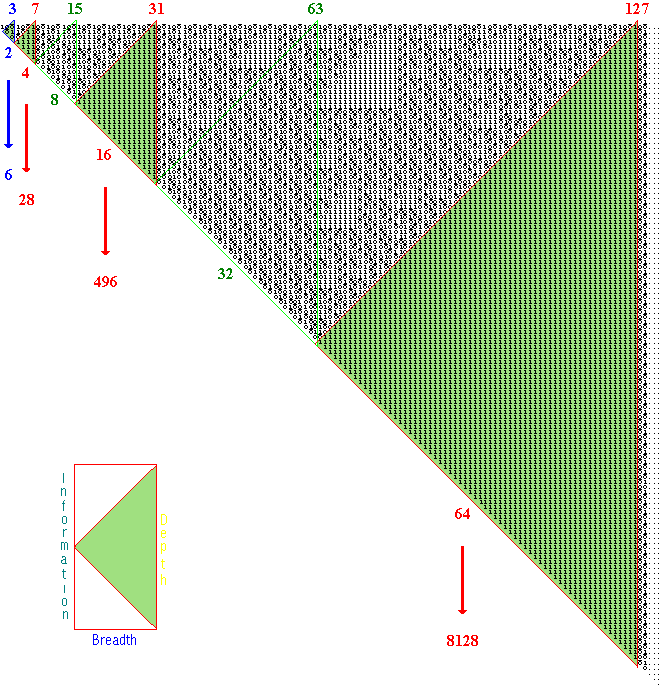
This series of triangles of 1's sharing the infinite edge of the infinitely expanding triangle created by the infinite sequential summing of the logical geometric series is the series of the edges of the triangles composed of the number of logical 1's in the geometric series x0, x1, x2, x3, . . ., where x = 16, that is, the series, 1, 16, 256, 4096, . . . (see illustration above). The triangles composing the series occupy the odd numbered places relative to the intervening groups of logical digits touching the edge of the major triangle. And each triangle is internally an expansion of logical 1's according to the ratio of the odd numbers, 1, 1 + 3 + 5 + 7, 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23 + 25 + 27 + 29 + 31, . . ., that is, according to the ratio of the distances traversed in successive equal intervals of time in Galileo's law of universal constant gravitational acceleration. Inspection of the pattern of triangles in this series shows that the longest edge of each of these triangles one of whose edges shares a portion of the infinite edge of the infinite triangular arrangement of digits is the first third of a three-digit column none of whose rows are composed of two or more consecutive 1's. The numbers of these three-digit columns correspond to the sequential summing of the series, x0, x1, x3, x5, . . ., where x = 2, the series, namely, 1, 1 + 2, 1 + 2 + 8, 1 + 2 + 8 + 32, . . ., or 1, 3, 11, 43, . . .. The defining longest edges themselves of the edge-sharing triangles are the single-digit columns whose places are determined by the sequential summing of the series, [(xy)0]½, [xy−1]½, [xy0]½, [xy1]½, [xy2]½, [xy3]½, . . ., where x = the area of the 576-entry-square of the infinite structure of existence6 and y = the area of that square's central square, 16, the series, namely, 1, 1 + 6, 1 + 6 + 24, 1 + 6 + 24 + 96, 1 + 6 + 24 + 96 + 384, . . ., or 1, 7, 31, 127, 511, . . .. This is the equivalent of determining the column number of the longest edge of any such triangle by calculating 1 plus the product of 1.5 and the sequential sum of the number of 1's contained in the edges of the edge-sharing triangles shared along the infinite edge up to and including the triangle under investigation. The column number of the defining longest edge = the number of 1's constituting that edge. Since the longest edge is the first third of a three-digit column none of whose rows are composed of two or more consecutive 1's, the following is the discernible analytic structure of the digits constituting each triangle in the series of edge-sharing triangles of 1's: 1 + 0, + 0 (the merely implicit triangle of 1's inaugurating the infinitely triangular order); 1 + 8, + 15; 1 + 224, + 255; 1 + 3968, + 4095; . . ., where 1 plus the second number subtracted from the total number of 1's in each triangle is the number of 1's in that triangle's longest edge, and 1 plus the third number is the total number of 1's in each triangle. The series which is composed of the sums of these elements of the successive edge-sharing triangles is 1, 24, 480, 8064, . . .. Where El is the number of 1's constituting the longest edge of an edge-sharing triangle and Es is the number of 1's constituting the edge of such a triangle shared with the infinite edge of the triangle created by the infinitely iterative summing of the trinary logic geometric series, Es = (El + 1)/2, and El × Es = the total number of digits in the infinite expansion up to and including the longest edge of the triangle under consideration. This total number of digits minus in sequence, beginning with the first edge-sharing triangle of 1's (shared edge = 4), the corresponding power of the series, x1, x2, x3, x4, . . ., where x = 4, = the sum of the elements of each edge-sharing triangle as analyzed, thusly, 28 - 4 = 24, 496 - 16 = 480, 8128 - 64 = 8064, . . ..
The infinitely expanding triangle created by the infinite sequential summing is a right-angled triangle each of whose legs is composed of the identical number of digits. This major triangle and each of its constituent triangular sets of 1's (for the two kinds of the latter see below) is thus a half-square. When the horizontal and vertical legs of this triangle are arranged so as to occupy the equal space corresponding to the equal number of digits in each, the infinite edge shared with the edge-sharing triangles -- the logical hypotenuse -- is to its geometric equivalent in the ratio 1 to 2½, taking the number of digits as its logical length. At the point of expansion defined by the longest edge of an edge-sharing triangle let that longest edge be the vertical leg, a, of the total triangular arrangement of digits. Then the arithmetic value of a = 2½ times the square root of the sum of .5 plus the sum of the elements of the edge-sharing triangle as analyzed above. The arithmetic value of the horizontal leg b = 1 + [2(a - 1)/3] and that of the hypotenuse c = b + [(a - b)/2].
The constant ratio of the total arithmetic value of the perimeter of the
infinitely expanding triangle to the total number of logical digits occupying it is, at
the point defined by the longest edge of each successive edge-sharing triangle of 1's,
![]() to 1, which is at once the ratio of the
arithmetic value of the three rows of the
cornerstone7 computed as end-overlapping sets to the total arithmetic value of those rows
calculated as discrete units, as well as 10 times the ratio of the successive edges of the
squares in the infinite structure of existence.8 The
difference between the total arithmetic value of this perimeter of the infinitely
expanding triangle of digits and the total number of digits on the perimeter at the point
defined by the longest edge is the number of 1's in the shared edge of that triangle minus
1, beginning with the first edge-sharing triangle (shared edge = 4) in accord with the
series, x1 - 1, x2 - 1, x3 - 1, x4 - 1, . .
., where x = 4. The difference between the total arithmetic value of the digits
interior to that total perimeter and the total number of interior digits increases,
beginning with the first discernible edge-sharing triangle (shared edge = 4), according to
the series, x1 - (x1 −1), x1 + x3 - (x2 - 1), x1 + x3 + x5 - (x3 - 1), . . ., where x = 4.
to 1, which is at once the ratio of the
arithmetic value of the three rows of the
cornerstone7 computed as end-overlapping sets to the total arithmetic value of those rows
calculated as discrete units, as well as 10 times the ratio of the successive edges of the
squares in the infinite structure of existence.8 The
difference between the total arithmetic value of this perimeter of the infinitely
expanding triangle of digits and the total number of digits on the perimeter at the point
defined by the longest edge is the number of 1's in the shared edge of that triangle minus
1, beginning with the first edge-sharing triangle (shared edge = 4) in accord with the
series, x1 - 1, x2 - 1, x3 - 1, x4 - 1, . .
., where x = 4. The difference between the total arithmetic value of the digits
interior to that total perimeter and the total number of interior digits increases,
beginning with the first discernible edge-sharing triangle (shared edge = 4), according to
the series, x1 - (x1 −1), x1 + x3 - (x2 - 1), x1 + x3 + x5 - (x3 - 1), . . ., where x = 4.
In addition to the infinite expansion of edge-sharing triangular sets of 1's, the infinitely expanding triangle created by the infinite sequential summing of the logical geometric series also contains right-angled non-edge-sharing triangular sets of 1's distributed between the occurrences of the members of the edge-sharing set. Where t1 is the total number of 1's forming a triangle of either kind and x is the number of 1's in the longest row of 1's in the triangle, then for non-edge-sharing triangles t1 = x + .5x(x−1) and for edge-sharing triangles t1 = x2. If in these formulas the extreme and mean ratio, φ, is allowed to equal x, then the ratio of [x + .5x(x−1)] to x2 = COS 36 (the central angle of the φ-structured regular decagon) = φ/2.
The total arithmetic value of the infinitely expanding
triangle of logical digits at the point of the longest edge of an edge-sharing triangle =
(El × Es) minus the increasing sequential sum of
the series, x1, x3, x5, x7, . . . .,
beginning with x1 for the
first discernible edge-sharing triangle (shared edge = 4), where x = 4. At the
limit of infinity the ratio of the total arithmetic value to the total number of logical
digits = ![]()
![]() π-.125. At infinity
the ratio of the total value of the edge-sharing triangles to the total number of digits =
.5, while the ratio of the total value of those triangles to that of the infinitely
expanding triangle of digits =
π-.125. At infinity
the ratio of the total value of the edge-sharing triangles to the total number of digits =
.5, while the ratio of the total value of those triangles to that of the infinitely
expanding triangle of digits =
 .9
.9
Finally, the absolute discontinuity of the continuum of the geometric series constituted by the series of edge-sharing triangles of 1's is demonstrated in the following way. All horizontally or vertically contiguous 1's in the array of digits produced by the infinite iterative sequential summing are members of a triangular arrangement of 1's. The edge-sharing triangles of 1's are exhaustively composed of such. But the digits between the triangles of 1's which share the infinite edge of the major expanding triangle can only be divided into triangles which reach from the latter's hypotenuse, c, to its horizontal leg, b, that contain horizontally or vertically contiguous 1's without containing the complete minor triangle of which the latter are elements. This feature of the infinite logical array, the perfect breaking of the continuum of the geometric series, is evident when one closely observes the earliest stages of the expansion, as here illustrated:
The total number of 1's in any group of digits lying between any two
nearest triangles of 1's sharing the infinite hypotenuse of the infinitely expanding major
triangle = 3 times the total number of digits in the expanding major triangle at the point
marked by the longest edge of the smaller of the two edge-sharing triangles, while the
total number of 0's and ![]() 's in any such group = 8 times the total
number of 1's constituting that smaller triangle.10 In
any such group the number of 0's = half that total of 0's and
's in any such group = 8 times the total
number of 1's constituting that smaller triangle.10 In
any such group the number of 0's = half that total of 0's and
![]() 's
minus 1, while the number of
's
minus 1, while the number of ![]() 's = half that total plus 1. The 1's
arranged in right-angled non-edge-sharing triangles appear in triangles whose bases are
composed of numbers of 1's found in the sequential summing of the series x1, x0, x1, x2, x3, x4, x5, . . ., where x = 2, beginning with x
for the group between the initial 1 of the major expanding triangle and the first
discernible edge-sharing triangle of 1's, and accumulating in each successive group by the
addition of triangles whose bases = the next 2 places in the sequentially summed series,
the numbers of triangles of each base in each group determined by size in descending order
as multiples in order of the series, x0, x1, x2, x3, x4, x5, . . ., where x = 3 (see
opening illustration). The total
arithmetic value of any such group (where Es−1 is the number of 1's constituting the shared edge of the smaller of the two
edge-sharing triangles) = Es−1(10Es−1 - 3).11 At infinity the ratio of the total arithmetic value of any two
larger and smaller successive groups of digits lying between edge-sharing triangles of 1's
is 16 to 1, the ratio of the successive edge-sharing triangles of 1's beginning with 1.
At infinity the ratio of discontinuity = the ratio of continuity. The ratio of the total
arithmetic value of the digits between any two nearest edge-sharing triangles of 1's to
the total arithmetic value of the expanding major triangle =
's = half that total plus 1. The 1's
arranged in right-angled non-edge-sharing triangles appear in triangles whose bases are
composed of numbers of 1's found in the sequential summing of the series x1, x0, x1, x2, x3, x4, x5, . . ., where x = 2, beginning with x
for the group between the initial 1 of the major expanding triangle and the first
discernible edge-sharing triangle of 1's, and accumulating in each successive group by the
addition of triangles whose bases = the next 2 places in the sequentially summed series,
the numbers of triangles of each base in each group determined by size in descending order
as multiples in order of the series, x0, x1, x2, x3, x4, x5, . . ., where x = 3 (see
opening illustration). The total
arithmetic value of any such group (where Es−1 is the number of 1's constituting the shared edge of the smaller of the two
edge-sharing triangles) = Es−1(10Es−1 - 3).11 At infinity the ratio of the total arithmetic value of any two
larger and smaller successive groups of digits lying between edge-sharing triangles of 1's
is 16 to 1, the ratio of the successive edge-sharing triangles of 1's beginning with 1.
At infinity the ratio of discontinuity = the ratio of continuity. The ratio of the total
arithmetic value of the digits between any two nearest edge-sharing triangles of 1's to
the total arithmetic value of the expanding major triangle =
![]() , so that the total arithmetic value of the larger
edge-sharing triangle of 1's equals the product of 16/10 and the total arithmetic value of
the group of digits lying between it and the smaller edge-sharing triangle of 1's.12
, so that the total arithmetic value of the larger
edge-sharing triangle of 1's equals the product of 16/10 and the total arithmetic value of
the group of digits lying between it and the smaller edge-sharing triangle of 1's.12
Real
Trinary Logic Matrix of the Perfect Numbers13
Where El is the number of digits constituting the longest edge of any edge-sharing triangle
(whether composed exclusively of 1's or composed of 0's, ![]() 's,
and 1's) and Es is the
number of digits
constituting the edge of such a triangle shared with the infinite edge of the triangle
created by the infinitely iterative summing of the trinary logic geometric series, Es = (El + 1)/2, and Es × El = the total number of digits in the
infinite expansion up to and including the longest edge of the triangle under
consideration. This cumulative total = the product of the total number of
digits in the longest edge of such a triangle times the number of digits that
share the edge of the major triangle. Thus the infinitely iterative
summing of the real trinary logic geometric series generates the matrix of the
series of perfect numbers. The perfect numbers -- 6, 28, 496, 8128,
33550336, 8589869056, 137438691328, 2305843008139952128,
2658455991569831744654692615953842176,
191561942608236107294793378084303638130997321548169216, . . . --
= the cumulative total of digits up to and including such a triangle where the
number of digits in the latter's longest edge is a prime number = the shared edge times the longest edge of that triangle, which,
beyond the exceptional and unique 6 whose precipitating prime = even number 2
and the quotient of the addition of whose factors divided by their product
(1+2+3)/(1×2×3) = 1, is always one of the series of edge-sharing triangles of 1's as here illustrated
's,
and 1's) and Es is the
number of digits
constituting the edge of such a triangle shared with the infinite edge of the triangle
created by the infinitely iterative summing of the trinary logic geometric series, Es = (El + 1)/2, and Es × El = the total number of digits in the
infinite expansion up to and including the longest edge of the triangle under
consideration. This cumulative total = the product of the total number of
digits in the longest edge of such a triangle times the number of digits that
share the edge of the major triangle. Thus the infinitely iterative
summing of the real trinary logic geometric series generates the matrix of the
series of perfect numbers. The perfect numbers -- 6, 28, 496, 8128,
33550336, 8589869056, 137438691328, 2305843008139952128,
2658455991569831744654692615953842176,
191561942608236107294793378084303638130997321548169216, . . . --
= the cumulative total of digits up to and including such a triangle where the
number of digits in the latter's longest edge is a prime number = the shared edge times the longest edge of that triangle, which,
beyond the exceptional and unique 6 whose precipitating prime = even number 2
and the quotient of the addition of whose factors divided by their product
(1+2+3)/(1×2×3) = 1, is always one of the series of edge-sharing triangles of 1's as here illustrated
Es × El = (2n−1)(2n−1)
The
arithmetic transcription of the logical digits (see above) comprising the edge
shared with the infinitely expanding major triangle by the very first
edge-sharing triangle (composed of two
![]() 's and a 0 and a 1) is
's and a 0 and a 1) is
![]() 0 = .5 + .5 = 1 = n−1. That of its longest edge is
0 = .5 + .5 = 1 = n−1. That of its longest edge is
![]() 10 = .5 + 1 + .5 = 2 = n. Thus the exceptional Es ×
El
real trinary logic form of this very first edge-sharing triangle
founds precisely the exception (n = 2) of the perfect number (2n−1)(2n−1)
= 2 × 3 = 6.
10 = .5 + 1 + .5 = 2 = n. Thus the exceptional Es ×
El
real trinary logic form of this very first edge-sharing triangle
founds precisely the exception (n = 2) of the perfect number (2n−1)(2n−1)
= 2 × 3 = 6.
The structural
economy of the logical form of this triangle -- whereby the arithmetic
transcriptions of the digits in the shared and longest edges the product of
whose numbers of digits equals the perfect number at once respectively equal n−1
and n -- is unique among all edge-sharing triangles in the matrix of perfect
numbers and founds the unique structural economy of the first such number
1+2+3 = 1×2×3 = 6.
In the thinking now occurring for the first time, where there is no nothing and 0 = not nothing,14 the body of bodies that is the universe is understood to be an infinitely flat surface15 whose structure is precisely a circular line or 'string' twisted upon itself and infinitely so, so that at infinity it is at once an absolute edge whose constituents are 'points' perfectly discontinuous, a line or 'string' composed of non-spatial non-tangent 'points'/surfaces, i.e., places, sans area, discrete, but without interstices––singularities in lieu of nothings. This absolute edge at once absolute singularity16 may be pictured abstractly as here illustrated (qua string the beginning could be made with a square,17 or, indeed, with any polygonal or non-polygonal shape enclosing an area, but the circle permits the simplest illustration), where the infinitely straight line produced by the expansion of the infinite geometric series of twisted circles (here shown in its relation to the perfect numbers together with which it is grounded in the infinitely expanding triangle produced by the iterative sequential summing of the real trinary logic geometric series) is, at the limit, the infinite repetition of the foundational fourfold18 actually beginning with the third twist in the fourth place:

where the bottom line is the absolute 'punchline' that is the body, the absolute multiplication that is the existing universe––the infinitely punctual line/the absolute(ly spaceless) time line—absolute singularity.
THEOREM:
There Are No Odd Perfect
Numbers
PROOF:
The infinite iterative sequential summing of the real trinary logic geometric series is the foundation of the numeric geometric series where x = 2, 22, and 24 (see infinitely expanding triangle first above).
2 and 3 are the only primes not a sum including some combination of two or more primes or reducible thereto. 2 = 1 + 1 = 0 + 2. 3 = 1 + 1 + 1 = 0 + 1 + 2. 2 is the perfectly compact base prime composed of no prime other than itself. 3 is the imperfectly compact base prime composed of 1 and a prime other than itself.
The singularity of the even prime is a function of its perfect compactness. The multiplicity of odd primes is a function of the odd base prime's imperfect compactness.
The perfectly and imperfectly compact base primes are intrinsic factors in the real trinary logic foundation of the numeric geometric series (ibid.) in the following ways:
Where x = the perfectly compact base prime 2 the foundational geometric series begins once and for all (perfectly): 1, 2, 4, 8, 16, 32, 64, . . . (as do likewise the series where x = 22 and x = 24).
Where x = the imperfectly compact base prime 3 the foundational geometric series begins an infinite number of times (imperfectly): 1; 1, 3, 9; 1, 3, 9, 27, 81; . . .. This series does not perfectly begin and does not infinitely end, i.e., is never complete. This series as such does not actually exist foundationally.
Perfect numbers must be prime number multiples of a member of a complete (actually existing) foundational geometric series (see infinitely expanding triangle last above).
Thus there are no odd perfect numbers.
The
Infinite Triangle & Logical Notation, Denotation,
Connotation, and Information
The longest edge of an edge-sharing triangle as defined above is the analogue of the logical depth or comprehension of a term and the shared edge defined above is the analogue of the logical breadth or extension of a term as these are understood by C.S. Peirce in "Upon Logical Comprehension and Extension," where logical area or information is understood to be logical breadth × logical depth.19
Concerning logical breadth Peirce says "that which can be predicated of whatever you please . . .has essential breadth," and "that of which you are at liberty to predicate what you please . . . has essential depth."20 In the case of the infinitely expanding triangle as delineated 2n−1 can be predicated of any member of the geometric series where x = 2, while a number of things can be predicated of 2n−1, for example, prime or not prime. Es × El = (2n−1)(2n−1) = the logical area or information dimension of an edge-sharing triangle = the total number of digits in the infinite expansion of the infinitely expanding triangle up to and including the longest edge of the edge-sharing triangle under consideration, and is a perfect number when a prime is the predicate of 2n−1.
As
illustrated to the lower left of the infinitely expanding triangle as last
depicted, in real trinary logic
0 (not nothing) can be taken to correspond to logical breadth,
![]() (not not nothing)
to logical depth, and the product of the former
0
(not not nothing)
to logical depth, and the product of the former
0![]() = 1 (not not not nothing) to logical
area.21
But, since 0 =
= 1 (not not not nothing) to logical
area.21
But, since 0 = ![]() = 1,
and
= 1,
and ![]()
![]()
![]() = 0, 000 =
= 0, 000 =
![]() , and
111 = 1,22 substantial unity of information additionally
involves logical height 1 as that the product of which and logical breadth and depth = the logical
volume of information 1 = 0
, and
111 = 1,22 substantial unity of information additionally
involves logical height 1 as that the product of which and logical breadth and depth = the logical
volume of information 1 = 0![]() 1,
at once the product of the cubes of the discrete logical roots of the latter 1
=
1,
at once the product of the cubes of the discrete logical roots of the latter 1
= ![]()
![]()
![]() 000111.
The identification of logical height 1, information
0
000111.
The identification of logical height 1, information
0![]() = 1, and volume of information 0
= 1, and volume of information 0![]() 1
= 1 at once the integration of the cubes of the
latter's roots
1
= 1 at once the integration of the cubes of the
latter's roots ![]()
![]()
![]() 000111
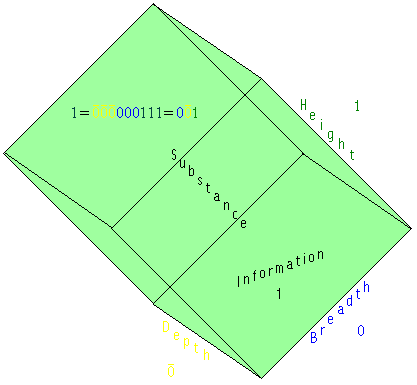
= 1, constitutes as such the Unity predicated of Four or the
categorical Fourthness in which the Third dimension is predicated of the Second, or
substance is predicated of information, as illustrated here23
000111
= 1, constitutes as such the Unity predicated of Four or the
categorical Fourthness in which the Third dimension is predicated of the Second, or
substance is predicated of information, as illustrated here23
Note that although for Peirce logical area or information is understood to be the product of logical breadth and logical depth,
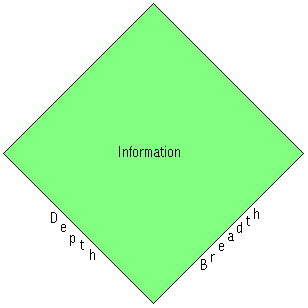
the product of denotation and connotation, the latter are themselves not derived but have an absolute status vis-à-vis information. Missing from this derivation of information is very notation (height). In real trinary logic depth (connotation) is derived from height (notation) and breadth (denotation). Information is the substantial product of denotation (breadth) and connotation (depth) when the last is the identity of very notation (height) with denotation (breath), as here illustrated

where the
(infinitely) linear structure that is no information (very breadth or
denotation) is imaged in two dimensions and the (infinitely) flat structure of
the real trinary logic series (1, 0,
![]() , 1 . . ., height, breadth, depth,
information . . ., analogue of the numeric geometric series) is imaged in three dimensions. Here what for Peirce would be
no information (very breadth or denotation without depth)24
is made
information in the medium of intelligibility (depth) that
is notation (height) identified with denotation (breadth). In the thinking
occurring before now very comprehension underived equaled no
information as did very extension underived. In the thinking now occurring
for the first time the identification of notation and denotation is the
comprehension that creates information where information was impossible when an
underived denotation was the counterpart of an underived comprehension.
, 1 . . ., height, breadth, depth,
information . . ., analogue of the numeric geometric series) is imaged in three dimensions. Here what for Peirce would be
no information (very breadth or denotation without depth)24
is made
information in the medium of intelligibility (depth) that
is notation (height) identified with denotation (breadth). In the thinking
occurring before now very comprehension underived equaled no
information as did very extension underived. In the thinking now occurring
for the first time the identification of notation and denotation is the
comprehension that creates information where information was impossible when an
underived denotation was the counterpart of an underived comprehension.
Notes
1 Cf. D.G. Leahy, Foundation: Matter the Body Itself (Albany, 1996),
Section IV.2, passim; cf. also, on this web,
The vmaxwell1/16
× 1 s/m Cube, Human Body Surface & BSA, &
the Infinitely Flat Structure of the Universe.
2 Cf. Leahy, Foundation, Section III.1.
3 Cf. Leahy, Foundation, Section IV.2, pp. 519ff.
4 The exponents of x here are actually the trinary logic arithmetic
series beginning with 0 plus the successive addition of 1 and the logical sorts of 1, 0
and ![]() , thusly, 0, (0)1, (01)0, (010)
, thusly, 0, (0)1, (01)0, (010)![]() , (010
, (010![]() )1, (010
)1, (010![]() 1)0, (010
1)0, (010![]() 10)
10)![]() , . . ., while the resulting trinary logic geometric series is actually
the series beginning with 1 successively multiplied by the trinary logic mean
proportional,
, . . ., while the resulting trinary logic geometric series is actually
the series beginning with 1 successively multiplied by the trinary logic mean
proportional, ![]() , and the logical sorts of
, and the logical sorts of
![]() , 1
and 0, thusly, 1, (1)
, 1
and 0, thusly, 1, (1)![]() , (1
, (1![]() )1, (1
)1, (1![]() 1)0, (1
1)0, (1![]() 10)
10)![]() , (1
, (1![]() 10
10![]() )1, (1
)1, (1![]() 10
10![]() 1)0. . .. For
1)0. . .. For ![]() as the radical mean between 0 and
1 in the logical order, cf. Leahy, Foundation, Section III.1, Note to Rule 5 (cf.
also Rule 6 and Note). See also, on this web,
Measure
Beyond Beyond Reach and
Real Trinary Logic, the
Imaginary Number i, & the Cyclic Series of Complex Numbers.
as the radical mean between 0 and
1 in the logical order, cf. Leahy, Foundation, Section III.1, Note to Rule 5 (cf.
also Rule 6 and Note). See also, on this web,
Measure
Beyond Beyond Reach and
Real Trinary Logic, the
Imaginary Number i, & the Cyclic Series of Complex Numbers.
5 Cf. Leahy, Foundation, Sections III.1 and IV.2. If 0 and
![]() are considered not in their equalizing arithmetic transcription but in
their purely logical distinction from one another, then the sequence of numbers of digits
in the pattern of sets of 1's and sets of 0's and
are considered not in their equalizing arithmetic transcription but in
their purely logical distinction from one another, then the sequence of numbers of digits
in the pattern of sets of 1's and sets of 0's and ![]() 's, along the
edge of the infinitely expanding major triangle, is the geometric series where x
= 2, i.e., the series which governs the process of cell multiplication from which all
organic life is built up, 1, 2, 4, 8, 16, 32, 64, . . .. So construed, the infinite
iterative summing of the trinary logic geometric series is at once the foundation of the
geometric series governing biological reproduction and growth. In this connection, see, on
this web,
The Rabbit Tree & The Logic of Life's Beginning
and
Beyond the Superego: The Pneumasomatic Human Person.
Also, for the trinary logic as template of the life of the Trinity, see, on this web,
Thinking Creation Ex Nihilo. For the
comparison of real trinary logic and the alternative duality-based ternary logic, see, on
this web,
Quantum Gravitational vs.
Quantum Logic: Virtually Left-handed Real Trinary Logic. In this
connection see also D.G. Leahy, Faith and Philosophy:
The Historical Impact (Aldershot, 2003), Chapter 7.
's, along the
edge of the infinitely expanding major triangle, is the geometric series where x
= 2, i.e., the series which governs the process of cell multiplication from which all
organic life is built up, 1, 2, 4, 8, 16, 32, 64, . . .. So construed, the infinite
iterative summing of the trinary logic geometric series is at once the foundation of the
geometric series governing biological reproduction and growth. In this connection, see, on
this web,
The Rabbit Tree & The Logic of Life's Beginning
and
Beyond the Superego: The Pneumasomatic Human Person.
Also, for the trinary logic as template of the life of the Trinity, see, on this web,
Thinking Creation Ex Nihilo. For the
comparison of real trinary logic and the alternative duality-based ternary logic, see, on
this web,
Quantum Gravitational vs.
Quantum Logic: Virtually Left-handed Real Trinary Logic. In this
connection see also D.G. Leahy, Faith and Philosophy:
The Historical Impact (Aldershot, 2003), Chapter 7.
6 Cf. Leahy, Foundation, Section IV.2.
7 Cf. Leahy, Foundation, Section III.1, et passim.
8 Cf. Leahy, Foundation, Section IV.2.
9 Where α and
δ are
the Feigenbaum "chaos" constants, 2.502907875095892 and 4.669201609102990, then
[(α + δ)/ ]4
]4![]() 829.441.5, exact to the fourth place (cf., on this
web,
Linguistic Correspondence to . . . [for 82944
see Leahy, Foundation, Sections III and IV, passim; also, on this web,
Thinking Creation Ex Nihilo,
The Higgs Boson & the Absolute Dead Center Cube: Predictions Within the Probable
Range,
Report
on a Dream & Related Matters & the God Particle,
82944 & the Four Fundamental Forces & the God Particle,
and
The Difference]).
829.441.5, exact to the fourth place (cf., on this
web,
Linguistic Correspondence to . . . [for 82944
see Leahy, Foundation, Sections III and IV, passim; also, on this web,
Thinking Creation Ex Nihilo,
The Higgs Boson & the Absolute Dead Center Cube: Predictions Within the Probable
Range,
Report
on a Dream & Related Matters & the God Particle,
82944 & the Four Fundamental Forces & the God Particle,
and
The Difference]).
 also has the following relations (where α is the fine structure
constant and φ is the
extreme and mean ratio):
also has the following relations (where α is the fine structure
constant and φ is the
extreme and mean ratio):
 .125/
.125/
![]() φ. LOG
φ. LOG
 −1
−1![]() 8.29441.5/100. LN
8.29441.5/100. LN
 −1
−1 ![]() (α × 10368.5)2. (φ
(α × 10368.5)2. (φ![]() )8
)8
![]() 82.944/9. 82.944α
82.944/9. 82.944α ![]() [1.1]½ ×
[1.1]½ ×  . (LOG
. (LOG
 /LOG .644476259278).25
/LOG .644476259278).25 ![]() 829.3184113/784
(where 829.3184113 is, with a difference less than 1 part per million, 1.11072073564, the 64th power of the ratio of the
circumference of the circle to the total length of the edges of its inscribed square). Finally, [LOG (.644476259278/
829.3184113/784
(where 829.3184113 is, with a difference less than 1 part per million, 1.11072073564, the 64th power of the ratio of the
circumference of the circle to the total length of the edges of its inscribed square). Finally, [LOG (.644476259278/ )]−1/64
)]−1/64
![]() (37 ×
(37 ×  )
)![]() /37
/37
![]() [1.1]½ (the
triple-cube body- face-diagonal ratio), and, where 10368.5 is the edge of the 'dead center cube',
[1.1]½ (the
triple-cube body- face-diagonal ratio), and, where 10368.5 is the edge of the 'dead center cube',
[(37 ×
 )
)![]() /37 × 1E33]−1/256/10368.5 = 0.007297 351 89,
/37 × 1E33]−1/256/10368.5 = 0.007297 351 89,
which is the value of the fine structure constant (0.007297 353 08)
exact to the 8th place (for the 37 logical diagonals of the triple-cube, see, on this web,
Logically Outfitted Cube(s),
Maxwell's Constant & the Trinary
Logic Triple-cube, and
The
vmaxwell1/16
× 1 s/m Cube, Human Body Surface & BSA, &
the Infinitely Flat Structure of the Universe; also
Leahy, Foundation, Section IV.2, p. 524, n. 98). For the physical
manifestation of the ratios  and
and
![]() as foundational in astronomy and
astronomically related areas of archaeology, see, on this web,
Sorted
Diagonals, Addenda. See also, on this web, The Langerhans-Epidermal Cell Ratio
& the Structure of the Epidermis.
as foundational in astronomy and
astronomically related areas of archaeology, see, on this web,
Sorted
Diagonals, Addenda. See also, on this web, The Langerhans-Epidermal Cell Ratio
& the Structure of the Epidermis.
10 At infinity the ratio in such groups of the number of 1's to the total
of 0's and ![]() 's is .75. Qua respective arithmetic values
the ratio of the total of 0's and
's is .75. Qua respective arithmetic values
the ratio of the total of 0's and ![]() 's to 1's in such
groups is
's to 1's in such
groups is ![]() . For the counterintuitive relationship of these
ratios in the prediction of body surface area, see, on this web, The Langerhans-Epidermal Cell Ratio & the
Structure of the Epidermis. .75 ×
. For the counterintuitive relationship of these
ratios in the prediction of body surface area, see, on this web, The Langerhans-Epidermal Cell Ratio & the
Structure of the Epidermis. .75 × ![]() = .5, at infinity the ratio of
the total value of the edge-sharing triangles to the total number of digits in
the major triangle (see above in the text). See also, on this web,
The Golden Bowl Structure: The Platonic Line,
Fibonacci, and Feigenbaum . For
= .5, at infinity the ratio of
the total value of the edge-sharing triangles to the total number of digits in
the major triangle (see above in the text). See also, on this web,
The Golden Bowl Structure: The Platonic Line,
Fibonacci, and Feigenbaum . For
 and the ratio of the values of
the elementary charge and gravitational constant, see, on this web,
Physical Variables,
Placedness, & the Absolute Dead Center Cube. For
and the ratio of the values of
the elementary charge and gravitational constant, see, on this web,
Physical Variables,
Placedness, & the Absolute Dead Center Cube. For
 and the
Beginning/Power Body ordered cornerstone, see, on this web,
The Real Beyond the Void: the
Beginning/the Power Body.
and the
Beginning/Power Body ordered cornerstone, see, on this web,
The Real Beyond the Void: the
Beginning/the Power Body.
11 Beginning at the point where the larger of the two is the first discernible
triangle of 1's (shared edge = 4), 10Es−1 - 3 is the series (where x = 4, y = 5 × 6, and z = 7), z,
z + y, z + y + x0(yx),
z + y + x0(yx) + x1(yx), z + y + x0(yx) + x1(yx) + x2(yx),
z + y + x0(yx) + x1(yx) + x2(yx) + x3(yx),
. . ., or, 07, 37, 157, 637, 2557, 10237, 40957, . . .. Beginning with the edge-sharing
triangle between the first two discernible edge-sharing triangles, note that the last two
digits of the successive factors are alternately 37 and (37 + 20 =) 57. 57/37 = 1 + 20/37,
where 20/37 is the ratio of the face diagonals to the total number of diagonals in the
trinary logically outfitted triple-cube (cf. above, n. 9, including the reference to
Leahy, Foundation).
12 Cf. above.
13 See also, on this web, Banach-Tarski Paradox & the Real Trinary Logic Matrix of the Fibonacci, Geometric, and Perfect Number Series.
14 Leahy, Foundation III.1. See also, on this web, Thinking Mathematics Sans Nothing.
15 Ibid., III.5, pp. 433ff.
16 See, on this web, The Simplicity & Syntax of the Concepts, Immediacy, Mediation, Omnipotence, & Beginning, where, effectively, singularity = placedness × particularity.
17 Leahy, Foundation IV.2, Excursus Circularis, pp. 535f., where the infinite straight line that is the circumference of Galileo's infinite circle is understood to turn "turning absolutely straight" qua the infinitesimal limit that is the fourfold minimum order, there initially a square inscribed within a circle.
18 Ibid., III.1, et passim.
19
C.S. Peirce, Writings of Charles S. Peirce: A Chronological Edition
Vol. 2 (Bloomington, 1984), pp. 70ff. Cf., also, D.G. Leahy, Beyond
Sovereignty: A New Global Ethics and Morality (Burlington and Aldershot,
2010), Section III.1-2.
20
Peirce, loc. cit.
21 For 0 = not nothing, etc., cf., above, n. 13, also, on this web,
Note to
Faith and Philosophy Further to the Ontology of Real Trinary Logic,
including further references.
22
Leahy, Foundation, Section III.1.
23
For 3 predicated of 2, cf., on this web,
Note to
Faith and Philosophy Further to the Ontology of Real Trinary Logic.
Also, for the minimum proportion 4 : 1 :: 2 : 3, cf. Leahy, Foundation,
Section III.1
24
Cf. Peirce, Writings, Vol. 2, p. 83: ". . . when there is no information,
there is either no depth or no breadth, and conversely."