The mathematical equation e^iπ + 1 = 0 is a particular instance of the equation x² + 1 = 0 whose solution is x² = −1, where x is the imaginary number i = √−1.¹

 

The imaginary number i is the generator in the cyclic series of complex numbers under multiplication by complex numbers.

 

The analogy between the cyclic series of imaginary numbers and the fourfold of real trinary logic elements, i : 0 (not nothing) :: −1 :    (not not nothing) :: -i : 1 (not not not nothing) :: 1 : 1, is illustrated, together with further logical, ontological, and geometric analogues, in this table where p = no negative and q = ordered/non-evental:²

  

 

 

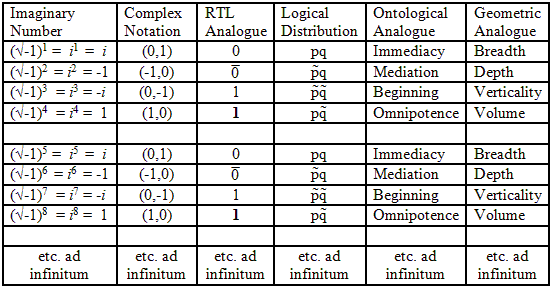
Note that an even exponent reverses the 0, 1 order and the sign of 1, as an odd exponent  reverses the 0, 1 order and the sign of i.

 

In ordinary mathematics it is true that x² + 1 = 0, whether x = i or x = -i.

 

i² = −1.  i⁴ = −1 × −1 = 1.  i × i³ = i × -i = i⁴ = 1.

 

At this point the analogy with real trinary logic breaks down.

 

Where i² = −1 =   , i⁴ = −1 × −1 =   = 1,

 

Where i = 0 and i³ = -i = 1, i × i³ = i × -i = 01 =  = i² = −1, that is, ≠  , ≠ i⁴, ≠ −1 × −1, ≠ 1.

 

In real trinary logic the participation of   is indispensable to the production of 1 involving 0 or 1.  01 =   = 1.  01 (i × i³) =   (i²) = −1.  [01 (i × i³) =   (i²) = −1] ×   (i²) = 01 (i⁴) =  (i⁴) = 1.

 

00 = 1 on condition that 00 = 0() = i × i⁶ = i³ = 1. 

 

11 = 1 on condition that 11 = 1() = i³ × i⁴ = i³ = 1.

 

00 = 1 on condition that 00 = ()() = i¹² = i⁴ = 1

 

11 = 1 on condition that 11 =   = i⁸ = i⁴ = 1

 

These equations call attention to the fact that where x is the exponent of i, and y is the numerator of the remainder in the division x/4,

 

i^x/i⁴ = i^y.

 

But then the proper understanding of the multiples of the imaginary number i is that they are elements in a geometric series whose underlying structure is the infinite repetition of the mathematical analogue of the real trinary logic minimum order, 1, 0,  , 1,³ that is, i⁰, i¹, i², i³ . . ., here illustrated:

 

 

 

 

Where the infinitely recurring imaginary number sequence is construed as the proportion, i⁰ : i¹ :: i² : i³ (= i⁴ : i⁵ :: i⁶ : i⁷, etc.), the linear product of this proportion  = i² (), the rational product = i² (), and the integral product = i⁴ () = 1.⁴

 

Real trinary logic provides the synthetic analysis of the otherwise apparent simple cycle in the powers of i so as to bring to the fore the difference between the sequence of the first three linear dimensions and the per se volumetric fourth dimension.  While a line times a second line perpendicular to the first = the first squared = depth, and a third line perpendicular to both the first and the second = the first raised to the third power = the vertical = the base for a volume bounded by depth, still, a volume not simply bounded by depth, but rather bounded by a volume bounded by depth, is not the product of breadth and the base for a volume bounded by depth—not the product of the first and third powers of the first line—but rather is a volume that = depth squared, clarifying the fact that i⁴ is not indifferently last in the sequence of the four dimensions. 

 

Real trinary logic constrains the recognition that the power of i apparently last in each cycle, Omnipotence (i⁴, i⁸, i¹², i¹⁶, . . .), is not in fact  last in the sequence, but always = i⁰, always in fact preceding Immediacy (i¹, i⁵, etc.), Mediation (i², i⁶, etc.), and Beginning (i³, i⁷, etc.), so that (not the fourth but) the second is the product of the first and the third,⁵ while the fourth is not directly that product but directly the product of that product squared.  Mediation raised to the second power (i⁴ =  ) = the product of Immediacy raised to the second power (i² =  ) and Beginning raised to the second power (i⁶ =  )—that is, i⁴ = i² × i⁶ = i⁸ = i⁰, that is, Omnipotence (i⁰ = 1).

 

The cyclic series of complex numbers under multiplication by complex numbers has been shown to be in fact a geometric series whose underlying structure is the infinite repetition of the mathematical analogue (i⁰, i¹, i², i³) of the real trinary logic minimum order (1, 0,   , 1).  Raising sequentially the infinitely cycling elements of this minimum fourfold order to the powers of the series of the three real trinary logical digits, 0,  , 1,⁶ likewise infinitely repeating, immediately produces the real trinary logic geometric series whose infinite sequential summing is the matrix of the mathematical geometric series and the series of perfect numbers,⁷ in such a way that the real trinary logic powers of 1 (1⁰, 1,  1¹, 1⁰, 1 ,  1¹, . . . = i⁰, i⁴, i⁸, i¹², i¹⁶, i²⁰, . . .) mark off the infinitely repeating sets of the bottom, middle, and top rows of the real trinary logic Cornerstone,⁸ as here illustrated:

 

     

             

 

Since e^iπ + 1 = 0 is a special case of Euler’s formula, e^ix = cos(x) + isin(x), where x = π, it can be readily seen that this relation of the logical powers of the 1 series to the real trinary logic geometric series is fundamental and sinusoidal.

 

In two dimensions, 1⁰ 0  ¹ 1⁰ 1,. . .  : 1 0 1 0. . .  :: sine wave : cosine wave:

 

 

 

 

Note also that sin(i)² + cos(i)² : 1 :: 1⁰ 0  ¹ 1⁰ 1. . . + 1 0 1 0. . .  : 1.

 

 

The Logical Double Helix, Transdecimal Calculation, & the Linear-Rational Differential of the DNA Molecule

 

 

When the two series are seen in three dimensions as the double helix — (e^iπ)(e^iπ) = (i²)(i²) = (−1)(−1) =  = 1 —  the repeating sequential sets of the bottom, middle, and top rows of the Cornerstone are likewise patent:

 

 

 

 

This double helix relates the sequence of the logical powers of the real trinary logic analogue of the cyclic sequence of complex numbers (1, 0,  , 1, 1,  . . . = i⁰, i¹, i², i³, i⁴,  . . .) to the real trinary logic geometric series (1, 0, , 1,  0, . . .), deriving, at once, the latter from the former.

 

In this outworking of the foundational analogy existing between the imaginary number i and the real trinary logic 0 (= not nothing) attention is called to three foundational relations.

 

First, the substantial analogy between the transdecimal calculation of numerical identity (linear product, rational product, integral product)⁹ and the structure of the molecule containing the genetic information for all stable living organisms.  As the transdecimal calculation of the integral product of the recurring fourfold cycle of the powers of i construed as a proportion [(i²)(i²) = i⁴] is produced by identifying the linear product (i⁰ × i¹ × i² × i³ = i²) with the rational product (i⁰ / i¹ × i² / i³ = i²),¹⁰ so in the basic arrangement of the genetic information of stable living organisms (the DNA molecule) the double helix consists in identifying the linear order (G, C, T, A, C, A, G, G, . . .) with the rational order (the pairing G:C, C:G, T:A, A:T, C:G, A:T, G:C, G:C, . . .).

 

Second, as in the double helix structure of the DNA molecule 3 hydrogen bonds hold the rational G:C pairs together and 2 hydrogen bonds hold the rational A:T pairs together, so in the logical double helix formed above there are 3 logical bonds between the 1’s in the series corresponding to the geometric series of the powers of i (1⁰ 0 ¹ 1⁰ 1 . . .) and 2 logical bonds between the 1’s in the derived real trinary logic geometric series (1 0  1 . . .).

 

Third, the number of logical bonds between the logical powers of the 1’s in one complete cycle of the logical double helix (1⁰ 0 ¹ 1⁰ 1 0^{1 0} 1 1¹ 0⁰  1¹ 1⁰)  is 9, corresponding to the number of atoms in each of the purine bases, linear A and G, while the number of logical bonds between the 1’s in one complete cycle (1 0  1 0 1 0  1) is 6, corresponding to the number of atoms in each of the pyrimidine bases, linear T and C.  Likewise (5C + 4C = 9C) : (4N + 2N = 6N) is the ratio of total carbon atoms to total nitrogen atoms in each of the rational G:C and A:T pairs.¹¹ 

 

Such is the logical structure of the linear-rational differential underlying the stability of the DNA molecule.