¹ Cf. D.G. Leahy, Beyond Sovereignty: A New Global Ethics and Morality (Aurora, 2010).

2 Cf. D.G. Leahy, Foundation: Matter the Body Itself (Albany, 1996), Section III.1.

3 Cf., above, nn. 1 and 2; also, D.G. Leahy, Novitas Mundi: Perception of the History of Being (Albany, 1994), "Prolegomena" and "Appendices α, β, and γ".

4 Leahy, Foundation, Section III.1.

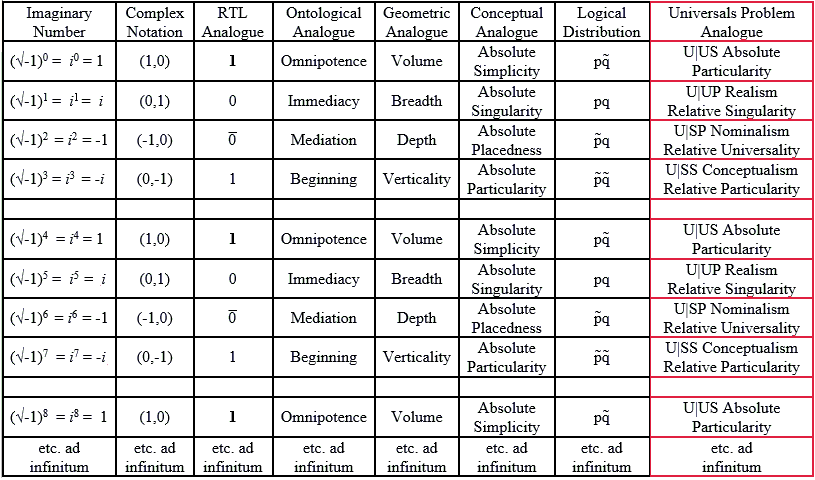
5 The reduction of the sequence pq + p̅q + pq̅ + p̅q̅ to the mathematical framework of the Cartesian coordinate system, + +, − +, + −, − −, makes it possible to elucidate the deep structure of the conceptualist equation S_r² = SS = (UP)².  In the sequence UP + SP + US + SS, when + and – are predicated of the respective elements qua unity, the last term SS is equivalently −1².  This S, the singular as such, is then, qua −1, the square of the imaginary number i = √−1: i² = (√−1)² = −1 (cf. the equivalents of the real trinary logic elements (1, 0, , 1) in Leahy, Beyond Sovereignty, Backnote 4, Table 4, et passim, and, on this web, Real Trinary Logic, the Imaginary Number i, & the Cyclic Series of Complex Numbers.  The singular as such −1, here, corresponds to absolute placedness i², on the scale employed loc. cit., the square of absolute singularity).  Thus the coherence of the conceptualist notion of the exhaustion of the generic in mente as the nameable whole radically imaginary is rendered patent: SS = −1² = (√−1)⁴ = i⁴ = (UP)² = 1² (cf., ibid., where i⁴  corresponds to Omnipotence).  

6 Transposing the OLO 1, 2, 4, 3 to the minimum order (MO) 4, 1, 2, 3 (cf., above, n. 2), the proportion U|US (Absolute Particularity) : U|UP (Realism) :: U|SP (Nominalism) : U|SS (Conceptualism) simplified by reduction to either S⁻¹ : P⁻¹ :: (SS) ⁻¹ : (SP)⁻¹ or −1 : 1 :: 1 : −1 proves in both forms to Unity (= i⁴, as above, n. 5).  Note that the penultimate form of the proportion confirms that Nominalism (the Real Unnameable) and Conceptualism (the Nameable Imaginary) are each the other’s reciprocal, respectively, (SS)⁻¹ and (SP)⁻¹.  The ratio (SS)⁻¹ : (SP)⁻¹ further simplified produces the ratio S⁻¹ : P⁻¹—transforming the reciprocal relation in the ultimate form of the proportion above (−1 : 1 :: 1 : −1) to identity (−1 : 1 :: −1 : 1) at once the form of the original proportion unreduced—precisely the form of the ratio of Absolute Particularity (the Real Absolutely Named) to Realism (the Real Nameable), the elements of which ratio are related as befits the ‘absolute originality’ of the MO ‘fourth/fourthness’ (cf. Leahy, Foundation, Section IV.1) not as essential reciprocals the one of the other but indeed as contradictories.  See, also, on this web, Real Trinary Logic, the Imaginary Number i, & the Cyclic Series of Complex Numbers where Omnipotence, on the scale there employed, corresponds to absolute singularity identified with absolute particularity as i⁴ = i¹ ∙ i³.  The conceptual correspondence here (OLO 4): U|US: the universal restricted to the singular identified with the universal, i.e., identified with the singular identified with the particular.  The ratio of Omnipotence (ibid.) to Absolute Particularity (U|US), i⁴/i², = Absolute Particularity (U|US), i².  This expanded version of the table(s) loc. cit. summarizes the complex (!) complex/noncomplex relationship between the two aforementioned scales of analysis

where (self-consciousness) "problem of universals" U|US Absolute Particularity (−1, as above, passim) corresponds to (other-consciousness) Absolute Placedness (−1) while nevertheless parallel to (other-consciousness) Absolute Simplicity (1 = i⁰ = i⁴) to neither of whose differentiated factors (Absolute Singularity [i¹] and Absolute Particularity [i³]) does it or any other element in the (self-consciousness) Universals Problem Analogue column correspond as such (cf., above, passim).  Thus is highlighted the radical removal foundational to self-consciousness at once from Immediacy (i¹ = i) and Beginning (i³ = -i).  Cf. G.W.F. Hegel's Gesamtwerk; also, D.G. Leahy, Faith and Philosophy: The Historical Impact (Aldershot and Burlington, 2003), "Appendix: Thinking in the Third Millennium: Looking Without the Looking Glass."

Vis-à-vis the ordinary logic of mathematical proportion note the following departure therefrom shared by the logic of complex numbers and the real trinary logic of the thinking now occurring:

 

1)  It is ordinarily true for all proportions composed of four discrete elements that the product of the lesser elements divided by the greatest element = the square of the least element.

 

2)  Where these discrete elements are related to one another by discrete powers of the antecedent in the ratio of the second to the first the underlying form of this constant is that of all logical statements pq, p̅q, pq̅, p̅q̅, where p = the first element not multiplied by x, and q = the first element not multiplied by y.  Thus, the aforementioned constant mathematical relation is logically equivalent to the relation (pq × p̅q × pq̅)/p̅q̅ = (pq)².

 

See, for example, on this web, Epitome or Food for Thought, the sequence, where x = 82944 and i(x) = the integral product of x (note: here i = integral product is not to be confused with i = imaginary number), [i(x)/9]/i[i(x)/9], i(x)/9, i(x), (i[i(x)/9][i(x)]) = 113.7̅7̅7, 9216, 82944, 6718464 = pq, p̅q, pq̅, p̅q̅, where p = 113.7̅7̅7 not multiplied by 9² and q = 113.7̅7̅7 not multiplied by 9³.  In accord with the stated rule, (pq × p̅q × pq̅)/p̅q̅ = (pq)², (113.7̅7̅7 × 9216 × 82944)/6718464 = 113.7̅7̅7².

 

Likewise, ibid., the sequence M (mass), M/T (mass flow rate), M/T² (surface tension), M/T³ (Poynting vector) = pq, p̅q, pq̅, p̅q̅, where p = M not multiplied by T⁻¹, and q = M not multiplied by T^-2.  In accord with the stated rule, (pq × p̅q × pq̅)/p̅q̅ = (pq)², (M × M/T × M/T²)/(M/T³) = M².  For fundamental M², cf. gravitational coupling constant αG = Me²/MP², as well as the imaginary mass of the Higgs field −M² and the real mass of the Higgs boson +M².

 

3)  But where i is the imaginary number, the sequence i, i², i³, i⁴ may be logically equivalent to pq, p̅q, pq̅, p̅q̅ (as above), but it may as well be equivalently pq, p̅q, p̅q̅, pq̅, where p = i not multiplied by i, since not previously so, or, since previously so multiplied, by -i, and q = i not multiplied by –i, and the relation between the last term and the product of its predecessors, productive of the square of the first term, (i ×  i² × i³)/i⁴ = i², will have the form (pq × p̅q × p̅q̅)/pq̅ = (pq)².

 

a)  On the analogy of the division in extreme and mean ratio whereby uniquely the whole line is divided but once to provide the elements of a geometrical proportion, so where p̅ and q̅ each ordinarily provide one of two multiples of i necessary to produce i⁴ the latter in the case of the cycle of imaginary numbers is nevertheless uniquely also able to be produced by multiplying but once by q̅. 

 

This logico-mathematical property is most perfectly realized in its real trinary logic analogue (cf., below, 3f).  For the relation of the extreme and mean ratio to the unique mathematics of the absolute dead center cube, see, on this web, Theorem & Proof: The Uniqueness of the Absolute Dead Center Cube and Ontic Ontological Logic of Human Sexuality & Word's Body The Medium The Message & The Messenger, Addendum V, et passim.  Cf., also, below, 3g.

 

b)  The relation of the real trinary logic elements 0, , 1, and 1, whose shared absolute value = 1 (cf. Leahy, Foundation III.1), may be compared to the complex numbers i, –1, –i, and 1, whose shared absolute value |z| = 1 in the unit circle of the complex plane, where, with respect to the complex numbers, p = relative value not negative, and q = relative value y > x, as here illustrated:

 

 

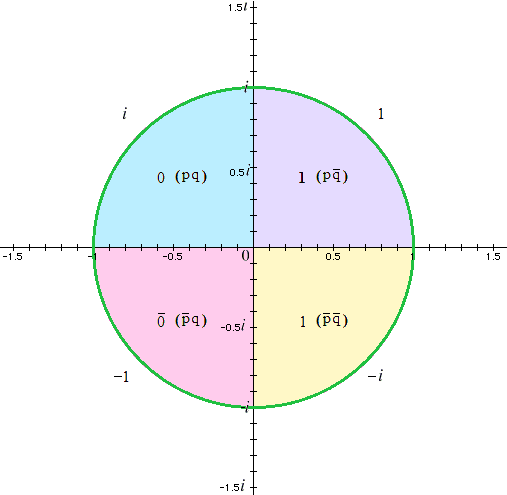
c)  The departure of the cycle of complex numbers from the ordinary logico-mathematical order of the form of proportions (above, para. 3), while real, is not unlimited.  While |z| = 1 is the shared absolute value of the complex numbers i, –1, –i, and 1 in the unit circle of the complex plane, the latter itself is not beyond the + and – framework of the x/y plane.  Where the complex numbers are grounded so, real trinary logic, on the other hand, is by analogy grounded in the always positive x > y pq̅ that is 1 = i⁴ and is, so grounded, consistently beyond the + and – framework of the x/y plane.

 

d)  That the complex plane falls short of the absolute indifference of the elements of real trinary logic to the + and – framework is demonstrable when real trinary logic  0 = 1 placed analogously alongside the x > y negative form i × –1 = –i (complex notation 0,–1) is positive (complex notation 1,0) and consistently so as 1    0 = 1 (complex notation 1,0) when placed analogously alongside the y > x negative form –i × –1 × i  = –1 (complex notation –1,0).

 

e)  In the case of the complex numbers where –i × –1 × i = –1 the end product is the included middle –1, i.e., the end product is not the excluded middle –i × i = 1.  Were the middle here the excluded middle then the end product would be –i × 1 × i = 1 = i⁴ = pq̅.   But, as it is, where the end product is the included middle –1, the end product is the return of the cycle itself upon itself in the form of the included middle, prematurely folding back upon itself perpetually foreclosing arriving at positive foundational unity 1.

 

In contrast, in the case of real trinary logic, where 1    0 = 1, the middle actually is the excluded middle, i.e., 1 0 = , and the end product of the threefold sequence is therefore the positive absolute foundational unity 1  (0  1)  0 =   = 1 = i⁴ = pq̅.

 

f)  Where 1 = i⁴ = pq̅, the real trinary logic end product immediately preceding, p = 0 not multiplied by 1, since not previously so, or, since previously so multiplied, by 0, and q = 0 not multiplied by .  In contrast, in the analogous construction above (para. 3) two multiples of i, viz., i and –i, the latter appearing twice, function in place of three multiples, since, as demonstrated above, there is no excluded middle in the threefold sequence of complex numbers.  But in the real trinary logic analogue to the aforementioned construction such a repetition of a second multiple in lieu of such a nonexistent excluded middle is absolutely obviated: the excluded middle  (demonstrably existent, as above,  ) appears independently as q̅ functioning together with 1 and 0 as one of three discrete logical multiples who share their absolute value +1 without any limitation whatsoever (cf., above, 3c).

 

g)  Summarily: (–i × –1 × i  = –1) : (1    0 = 1) :: not having happened as of now having not ceased as of now (Mediation) : having happened as of now having ceased as of now (Omnipotence) :: perpetual unity in the negative : perpetually positive absolute unity :: relative discontinuity of the continuum : absolute discontinuity of the continuum :: included middle : excluded middle :: cycle/circle perpetually recommencing : cycle/circle always and everywhere an absolutely new beginning :: dyadic ternary logic : real trinary logic :: ordinary geometric proportion : division in extreme and mean ratio (cf., above, 3a).

 

For mediation and omnipotence, and relative vs. absolute discontinuity of the continuum, cf. Leahy, Beyond Sovereignty, passim, for the former and the latter, and Backnote 4, Tables 1-2, for the former. For the excluded vs. included middle, cf. Leahy, Faith and Philosophy, Chapter 7.  For dyadic ternary vs. real trinary logic, cf. Leahy, Foundation III.1, Afterword 2, and “Appendix: The De Trinitate of Augustine and the Logic.” 

4)  Where the cyclic relation of the powers of i is understood as this logico-mathematical departure from the ordinary form a discretionary contextual relation surfaces that makes a real logico-mathematical difference as p̅, whose configuration here is fully consonant with the real trinary logic fundamental operator  ‘since’ (cf. Leahy, Foundation, Section III.1, and, above, passim), at once with the first appearance of p̅ in the "Index of the Ethics of Simplicity" indeed in association with Discretion p̅q (see, on this web, Beyond the Superego: The Pneumasomatic Human Person). 

5)  Cf. also the table above, where, on the analogy to i in the cycle of complex numbers, the logical equivalent of Omnipotence is pq̅ = i⁴, related as such to Immediacy pq = i, Mediation p̅q = i², and Beginning p̅q̅ = i³, and compare this with, on this web, ibid., "The Index of the Ethics of Simplicity," where, likewise, the logical equivalent of Omnipotence is pq̅, related as such to Readiness pq, Discretion p̅q, and Beneficence p̅q̅, where p = not discriminating, and q = not doing.

⁷ For the identity of concept and percept, cf. Leahy, Foundation, passim.