EPIDERMAL IMMUNITY STRUCTURE & THE ABSOLUTE DEAD CENTER
HYPERCUBE VOLUME/BOUNDARY RATIO
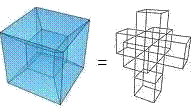
All biological surface is concrete, and, unlike the abstract surface of a sphere or a cube, has, qua surface, volume. The volume per se of a cube : hypercubic surface volume :: hypercubic surface volume : the unimageable volume of the hypercube. The proof-form of this proportion: cubic volume per se identified with unimageable hypercubic volume has as its predicate existent hypercubic surface volume. Surface that, qua surface, has volume is, in the first instance, the 8-fold surface of the hypercube:

which surface = 8x3, and is not to be confused with the undrawable volume of the hypercube itself = x4. These 8 imageable cubes + the 1 unimageable hypercube volume––the hypercube boundary + the hypercube volume––constitute a 9-fold analogous to the 9-fold real trinary logic cornerstone (see, on this web, The Cornerstone).
Cf. Dali's Corpus Hypercubus (see, on this web, Dali Crucifixion [Corpus Hypercubus]):

where the Corpus Christi is in the place of the 9th element — the unimageable hypercube volume — compared to the describable 8 cubes constituting the hypercubic surface. Of this painting Dali himself said: "The number nine is identifiable and becomes especially consubstantial with the body of Christ."
Where x4 is the absolute dead center hypercube volume (see, on
this web,
Theorem & Proof: The Uniqueness of the
Absolute Dead Center Cube), Dali's 9 "consubstantial with the body of
Christ" identified in turn with the absolute dead center hypercube volume, 9x4, is the hypercube volume whose base is the
body-diagonal of the absolute dead center cube (cf. D.G. Leahy, Foundation:
Matter the Body Itself [Albany, 1996], Section III.5, pp. 434ff.). In
this connection, compare the substantive analogue in Thomas Aquinas' hymn,
Panis Angelicus, where panis coelicus ("heavenly
bread" = Corpus Christi) puts an end to forms (dat . . . figuris terminum),
as the unimaginable hypercubic volume (= Dali's 9 "consubstantial with the body
of Christ") puts
an end to the imageable volume of the hypercubic surface.
On the analogy to x4/i(x4) = 82944/784 (see, on this web, Measure Beyond Beyond Reach),
9x4/i(9x4) ~ 75346/17778,
where on the right side of the equation the antecedent is the number of FEU Malpighian (living) cells and the consequent is the number of (dead) cells in the FEU stratum corneum (see, on this web, The Langerhans-Epidermal Cell Ratio & the Structure of the Epidermis; cf., also, S.B. Hoath and D.G. Leahy, “The Organization of Human Epidermis: Functional Epidermal Units and Phi Proportionality,” The Journal of Investigative Dermatology 121, 1440−1446 [2003]).
Where i(9x4) is the integral product of the 9x4 hypercube volume, 8[√3(x)]3 its surface volume, and 93124 (= 75346 + 17778) the total number of FEU cells,
i(9x4)/8[√3(x)]3 ~ 93124/17778.
The total number of cells in the epidermal Langerhans unit (whose surface is the inner epidermal immune barrier; cf. S.B. Hoath and D.G. Leahy, "Formation and Function of the Stratum Corneum," in The Essential Stratum Corneum [Informa Health Care, 2002], pp. 31-40) is a function of the product of the unique absolute dead center hypercubic Volume/Boundary ratio x4/8x3 = 1621/2 (see, on this web, Theorem & Proof: The Uniqueness of the Absolute Dead Center Cube) and the FEU ratio of Malpighian (living) to stratum corneum (dead) cells (the latter the outer epidermal immune barrier):
1621/2 × 75346/17778 ~ 54.