c)1/2,4
and qP
and the Planck length, lP,
are substituted for Q and L in the bridge ratio, Q4/L3,
and (x/6)4/x3 is the fourth-power
volume/surface ratio of the absolute dead center cube divided by the cube
volume,
THE MAGNITUDE OF BEING
The Rydberg constant, R∞ = 1.0973731568527 × 106 dm−1 (CODATA 2006), is equal to the product µ02c3e4me/8h3. R∞ is the constant of magnitude of atomic and molecular energy levels (The NIST Reference on Constants, Units, and Uncertainty). R∞ assumes a hypothetical infinite nuclear mass (compare this to the infinite density of the finite sphere in the Banach-Tarski paradox: Banach-Tarski Paradox & the Real Trinary Logic Matrix of the Fibonacci, Geometric, and Perfect Number Series). Note that [ρ = m/V] → [ρ∞ ↔ m∞]. The R∞ infinite mass assumes V = 0, and, therefore, infinite density. The infinite density of the Banach-Tarski sphere assumes V > 0, and, therefore, infinitely infinite mass, infinite mass squared.
Dimensional Analysis
Ignoring the purely numerical multiples, µ0 and 8 (µ0 = permeability of free space, exactly 4π × 10-7),1 reduce the Rydberg constant to its pure physical dimensions, where L = length (m), M = mass (kg), T = time (s), and Q = (ML)1/2 = charge:2
(L/T)3Q4M/(ML2/T)3,
(L3/T3)Q4M/(M3L6)/T3,
L3Q4M/(M3L6),
Q4/(L3M2),
(M2L2)/(M2L3),
L−1.
Cf. D.G. Leahy, Foundation: Matter the Body Itself (Albany, 1996), pp. 132ff., “The absolute measure of the magnitude of being,” where m = mass, c = velocity of light, T = time, and L = length:
m2/Tc,
m2/T(L/T),
m2/L,
Q4/L3.
The absolute measure of the magnitude of being = the finite measure of the magnitude of being (m2)3 identical with the infinite measure (L−1):
m2/Tc = Q4/L3 = [Q4/(L3M2)]M2 = m2/L
Compare the unique constitutionally perfect hypercubic structure of the absolute dead center cube (Theorem & Proof: The Uniqueness of the Absolute Dead center Cube), where, when x = 103681/2,
(x/6)4/x3 = 8x3/x4.
Employ the following analogy: let (x/6)4/x3 = M and 8x3/x4 = L. Then for all cubes (x/6)4/x3 × 8x3/x4 = ML. Unlike all other cubes, for the absolute dead center cube (x/6)4/x3 = 8x3/x4 = (ML)1/2. This analogue illustrates how the unique hypercubic structure of the absolute dead center cube is the formal template for understanding Q = (ML)1/2 = charge.
Ignoring the non-linear factors, 6 and 8, note also the analogy between the linear ratio x4/x3, the e4/h3 dimensional ratio integral to the Rydberg constant, and “the absolute measure of the magnitude of being,” the bridge ratio, Q4/L3, the volume density of hypercubic (infinitely flat) charge.
_____________________________
Beyond the formal analogy, note that where x4 = the volume of the absolute dead center hypercube, i(x4) = the integral product of that volume (Measure Beyond Beyond Reach), and R∞ = 1.0973731568527 × 106 dm−1,
R∞ dm/x2 ~ x4/i(x4) = 82944/784,
the ratio uniquely that of the absolute dead center hypercube volume to its integral product (ibid.)—with a difference ~ (829.44/784)128−1 ~ (e4/h3)(8∙128∙128)−1 × ML3/T3.
Where the Planck charge qP
= (4πε0c)1/2,4
and qP
and the Planck length, lP,
are substituted for Q and L in the bridge ratio, Q4/L3,
and (x/6)4/x3 is the fourth-power
volume/surface ratio of the absolute dead center cube divided by the cube
volume,
[qP4/lP3 × (x/6)4/x3](4∙4)−1 × (M2/L)−1 ~ 82944/784,
and, since (x/6)4/x3 = 8x3/x4 = (ML)1/2 (the formal analogue of Q = charge, as above), where 8x3/x4, the surface/volume ratio of the absolute dead center hypercube, is substituted for (x/6)4/x3,
[qP4/lP3 × 8x3/x4](4∙4)−1 × (M2/L)−1 ~ 82944/784,
with a difference in both cases ~
1 + [(qP4/[x/6]4)(4/128) × (M2L2)−1] = 1 + [(qP4/82944)(4/128) × (M2L2)−1].
_____________________________
Since [(x/6)4/x3]2 = [8x3/x4]2, by analogy (as above) M2 = L2,5 at once ML = ML, the unique hypercubic structure of the absolute dead center cube shows it to be not only the absolute balance point in the infinite array of all cubes (Theorem & Proof: The Uniqueness of the Absolute Dead Center Cube; illustrated in 2 dimensions)
but as the center for all cubes at once the fundamental template for the formula determining the center of mass where m = mass, and R, r, = the position vector:6
simplifying, transposing, and substituting M for m = mass and L for R, r, = the position vector,
ML = ML.
The physical,
non-tautological, nature of this otherwise purely formal equation is a function
of the fact that, by analogy (as above), M = L = (ML)1/2. In
turn, the unique rational constitution of the absolute dead center cube is
founded in the operations of real trinary logic, where, since 00 =
.gif){kind=small}
= 0
= 1, 0 = =
0.
For all cubes
other than the absolute dead center cube, although ML = ML, M ≠ (ML)1/2
and L ≠ (ML)1/2. The rationally unbalanced constitution of these cubes
inadequate to the real balance of physical forces is
consistent with dyadic trinary logic, where, although 0U = 1, since 00 ≠ UU ≠
0U, 0 ≠ U ≠ 0U.7 See, on this web,
Quantum Gravitational vs. Quantum Logic:
Virtually Left-handed Real Trinary Logic.
_____________________________
Cf. Leahy,
Foundation, Section IV.2, pp. 519-29, where the L series
is the arithmetic transcription of the sequential summing of the real
trinary logic geometric series, 1, 0,
, 1, 0,
, 1, 0,
, . . ., that is, 1,
1.5, 2, 3, 3.5, 4, 5, 5.5, . . .. The inverse alternating L series,
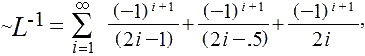
= .6444762592780 . . ..
Recall that the fourth-power volume/surface ratio of the absolute dead center cube divided by the cube volume, (x/6)4/x3, = the surface/volume ratio of the absolute dead center hypercube, 8x3/x4.
Where gravitational force = centripetal force, G is the gravitational constant, (x/6)4/x3 and 8x3/x4 the uniquely equal elements of the absolute dead center cube (the balance point of the infinite array of cubes), and ~L−1 the inverse alternating L series,8
[(x/6)4/x3 × ~L−1]−1 + [8x3/x4 × ~L−1]−1 ~ 4π2 = G(M + M)T2/L3,
which is Newton’s refinement of Kepler’s 3rd law, viz., that the cube of the radius of the orbit is proportional to the square of the period for all pairs of objects orbiting their center of mass.
Since
G(M)T2/L3 = (L3/MT2)[(M)T2/L3],
the gravitational/centripetal force reduces by dimensional analysis to a function of the unique purely geometric dimensions of the absolute dead center cube:
[(x/6)4/x3 × ~L−1]−1 + [8x3/x4 × ~L−1]−1 ~ 4π2 = 2π2 + 2π2.9
_____________________________
Here is a wide-angle partial view of the Plot for (x/6)4/x3 = 8x3/x4, showing the semi-axis lengths [4 | 4] and the focal parameter [2 √2 = 2.828427125 = 81/2]:
When Einstein’s
field equations are expressed in
geometrized units, the circumference of the circle intersecting the (x/6)4/x3 = 8x3/x4
hyperbola = the ratio of the curvature of spacetime to its matter/energy
content:
Notes
1 µ0 = 4π × 10−7 N·A−2. Cf. http://en.wikipedia.org/wiki/Magnetic_constant, http://en.wikipedia.org/wiki/Newton_(unit), and http://en.wikipedia.org/wiki/Ampere. In keeping with the dimensional analysis here employed, 1 N = 1 kg m s-2 = 1 ML/T2 and 1 A = 1 C s−1 = 1 (ML)1/2/T, N·A−2 = (ML/T2)/(ML/T2) = 1.
2 Cf., on this web, Common Biophysical Variables as Combinations of Planck Length (lp), Planck Time (tp) and Planck Mass (mp) & the Equivalent Golden Section Factors, (prepared by S.B. Hoath). For the choice of the ampere as the basic SI unit of electric current and its historical relation to the dimensional notion of charge, cf. H.A. Klein, The World of Measurements (New York, 1974), pp. 427ff.
3 For m2, cf. N. Redington and M.A.K. Lodhi, “Discrete Character of Meson Masses.” Online at: http://web.mit.edu/redingtn/www/twolines.pdf. March 2010.
4 qP
= (4πε0c)1/2
= 1.875545870 × 10−18 C. Cf.
http://en.wikipedia.org/wiki/Planck_units. For an analysis of the
exceptional mathematical derivation of this value of qP—inconsistent
with that of the values of the other Planck units—and of its substitution in the
scientific literature for 5.93089 × 10-22
C (see, above, n. 2), cf.
http://www.earthmatrix.com/sciencetoday/planckunits/planck_unit.pdf.
Put in the simplest terms,
qP
= (4πε0c)1/2
= 1.875545870 × 10−18 C, when,
effectively, c
= 2.997924580 × 109 dm s−1. This measure neatly fits with
the ratio R∞ dm/x2 ~ x4/i(x4)
= 82944/784. When, effectively, c = 2.99792458 × 102 Mm
s−1, qP
= (4πε0c)1/2
= 5.93089 × 10-22 C.
For a proposal to fix the Planck charge at qP
= (2ε0hc)1/2,
where c
= 2.99792458 × 108 m s−1, cf.
http://iopscience.iop.org/0026−1394/43/6/014/pdf/met6_6_014.pdf?ejredirect=migration.
5 Compare the ratio, M2/L2 = 1, to the fundamental logical ratio i2/j2 = 1, the proof form of the "unity of the minimum order of the elements of the foundation" (cf. Leahy, Foundation, pp. 276ff.; also, pp. 387ff., pp. 399ff., and pp. 491ff.). See also, on this web, The Deep Epidermal Surface: The Cornerstone Construction Order, Minimum Order Tetrahedron Hypercube, & Absolute Dead Center Hypercube.
6 Cf. http://en.wikipedia.org/wiki/Center_of_mass.
7 For a different approach to M = L, see, on this web, Theorem for a Flat Universe: The ρcrit = 3H02/8πG Building Block 1000.125.
8 ~L−1 = .6444762592780 . . .. The rational product of the Hebrew נקדת העיון, ‘point of balance’, = 33.6−1 and the rational product of יחוס, ‘relation’, = 8−1. Consonant with its function in what immediately follows, ~L−1 = .6444762592780 . . . ~ (33.6−1)8−1 = יחוסנקדת העיון, ‘point of balance’ raised to the ‘relation’ power. Cf. Leahy, Foundation, pp. 521ff. For the new, essentially rational, reading of the mathematics of the ancient languages, see, on this web, Transdecimal Calculation of Number Identity: A Note on Integral Product & Related Terms. Where the electric constant ε0 (see the Planck charge, above, n. 4) = 8.8541878176 × 10−12 F/m, 144π = the circumference inscribing the face of the absolute dead center cube = the area of each of the circles inscribing each of the 36 equal parts of that face (an identity unique to the absolute dead center cube [cf. Leahy, Foundation, p. 524, n. 98]), and ~L−1 = .6444762592780, then (~L−1)16/(144π)(162∙82)−1 × 10-8 F/m = ε0, accurate to 1 part in 10 million. Further for ~L−1, see, on this web, The Diagonal Logic of the Triple Absolute Dead Center Cube & Certain Fundamental Mathematical & Physical Constants.
9 4π2 =
2π2 + 2π2 = the total
surface area of two 4D unit hyperspheres.
10 Cf.
http://en.wikipedia.org/wiki/Einstein_field_equations. See also,
on this web,
Sorted Diagonals,
Addenda 2000-2006, 3.
.